|
JOSHY.K.J Assistant Professor Department of Economics Christ University, Bangalore-560029 Contact No.- 08040129718 (Office), 9916990522 (Mobile) Email: joshy.kj@christuniversity.in |
GANESH.L Associate Professor Institute of Management Christ University, Bangalore-560029 Contact No.- 08040129522 (Office), 9900733882 (Mobile) Email: ganesh.l@christuniversity.in |
The study aims at analyzing the price discovery process of gold in Indian commodity market. It also examines the long run dynamic relationship between spot and futures markets and looks into the volatility impact of futures price on spot price as well as the volatility impact of spot price on futures price. The study is based on the secondary data obtained from the official website of NCDEX during 2008 to 2012. In order to test the hypotheses different econometric tools are employed. The Johansen co-integration reveals the dynamic relationship between spot and futures markets. The results of VECM indicate that the spot market is dominant in the price discovery process. It implies the information efficiency of spot market. The findings of GARCH model highlight the significant price volatility impact of both futures and spot market prices on the returns. The findings are very significant for investors, marketers and policy makers since it provides a reliable forecast of spot prices in the future which allow them to effectively manage their risks in the production and marketing process. The unprecedented uptrend and high volatility in the gold prices in recent years has very significant social implications too.
GEL Classification: G12, G13, G14
Key words: Price discovery, GARCH, VECM , Price volatility, Market efficiency.
The broadest classification of the Indian financial market can be made in terms of commodity market, stock and security markets and foreign exchange market. Commodity markets are markets in which primary products are exchanged on regulated commodity exchanges through standardized contracts. The transformation of Indian economy with globalization move has made the commodity markets more structured and systematic. The introduction of gold futures trading has brought the integration of demand and supply of market participants. The three major commodity exchanges operating in India are Multi-Commodity Exchange (MCX), National Commodities and Derivatives Exchange (NCDEX) and National Multi-Commodity Exchange of India Ltd. (NMCEIL). The commodities and the futures market in the country is regulated by Forward Markets Commission (FMC). India is the largest consumer of gold in the world accounting for nearly 25 percent of the total gold consumption which is mainly in the form of jewellery and investment demand. Indian gold demand is supported by cultural and religious traditions which are not directly linked to global economic trends. Thus demand remains steady even during high prices. The steadily rising prices of gold reinforce the inherent value of gold, an intrinsic part of its desirability and also as a means of investment.
It is often said that gold price is a good indicator of the health of the economy. When the price of gold is on a rise, it indicates adverse health for the economy. That means the investors flock to gold in order to protect their investments from either a crisis or inflation. When gold prices drop, that usually signals the economy is healthy because investors leave gold for other, more lucrative, investments like bonds or real estate. On the demand side, factors like rise in investor demand, Jewellery demand, technological demand, geo-political concerns, US dollar movement against other currencies, Indian rupee movement against the US dollar and Central Banks diversifying into bullion are very significant. On the supply front factors like slowing Central Bank sales, massive de-hedging, gold mine production are important. The main sources of supply of gold are mine production and recycling of (used) gold.
Price discovery is a mechanism to determine the price of an asset or a commodity in the market place through the interactions of buyers and sellers. It helps in identifying whether the spot market dominates the futures market or the futures market dominates the spot market. It involves buyers and sellers arriving at a transaction price for a specific item at a given time. In a dynamic market, the price discovery takes place continuously. It helps in finding the exact price for a commodity or a share based on inputs regarding specific market information, the demand and supply equilibrium, weather forecasts, expert views and comments, inflation rates, government policies, market dynamics like hopes and fears, futures trading and so on. This transforms in to continuous price discovery mechanism. Spot contract or spot transaction is a contract of buying or selling a commodity, security or currency for settlement (payment and delivery) on the spot date, which is normally two business days after the trade date. The settlement prices are called spot price. Commodity futures contract refers to an agreement to buy or sell a set amount of a commodity at a predetermined price and date. Unlike cash markets a futures market is based on buying (or selling) commodity contracts at a fixed price for potential physical delivery at some future date.
Volatility measures the variation of price of a financial instrument over time and is used to quantify the risk of the financial instrument. It is normally expressed in annualized terms, and it may either be an absolute number ($5) or a fraction of the mean (5 percent). It refers to the relative rate at which the price of a security moves up and down. It is found by calculating the annualized standard deviation of daily change in price. It can either be measured through the standard deviation or variance between returns from that same security or market index. It is influenced by factors such as investor confidence, direct or implied government intervention, uncertainty, booming and bursting bubbles and noise trading. There exists a direct relationship between volatility and risk from a particular security. Higher the volatility, the riskier the security is. Correspondingly, there is an inverse relationship between volatility and return from a financial asset since there is a positive relationship between risk and return. Positive trends are said to be existed when the futures prices are greater than spot price. Generally investors take decisions based on positive trends. Negative trends signal higher amount of volatility and irrational behaviour of investors in the markets.
Kushankur. D and Debasish. M (2012) inferred that unidirectional causality from futures to spot prices has been observed in the Indian pepper futures market and the adjustment of innovations or shocks in the futures market is relatively faster than that of the spot market. Srinivasan P (2012) observed that there is a flow of information from spot to futures commodity markets and bidirectional volatility spillover persists between the markets. Sarkar A.K, and Shailesh Rastogi (2011) found that the introduction of gold and silver futures in India has increased the depth of the market and has helped in the price discovery in the spot market but without impacting price volatility. Pantisa Pavabutr and Piyamas Chaihetphon (2010) examined the price discovery concluding that futures prices of both standard and mini contracts lead spot price. Vishwanathan Iyer and Archana Pillai (2010) found evidence for price discovery in the futures market in five out of six commodities including gold. Biswat Pratap Chandra (2009) concluded that futures and spot markets are co integrated and sharing a long run relationship with a causality flow from futures markets to spot markets indicating information flow from futures to spot markets. R.Salvadi Easwaran and P. Ramasundaram (2008) indicated that the futures and spot markets are not integrated in agricultural commodities and the market volume and depth are not significantly influenced by the return and volatility of futures and spot markets. Golaka.C.Nath and Tulsi Lingareddy (2012) explored the effect of the introduction of futures trading on spot prices of pulses and found that futures volumes had a significant causal impact on spot prices and not vice versa. Sahi G.S (2006) analysed the impact of introducing futures contracts on the volatility of the underlying commodities and observed the destabilizing effect of futures trading on spot prices of commodities. Yang J, Balyeat B, and Leatham D. J (2005) indicated that an expected and unidirectional increase in futures trading volume drove cash price volatility up. Fu and Quing (2006) found the long term equilibrium relationships and significant bidirectional information flows between spot and futures markets, with futures being dominant. Zhong, Maosen, Ali F. Darrat and Rafael Otero (2004) concluded that the futures price index was a useful price discovery vehicle and futures trading had been a source of instability for the spot market. M.T. Raju and Kiran Karande (2003) found that the futures market responds fast to deviations from equilibrium and the price discovery occurs in both the futures and the spot market.
The recent global meltdown has witnessed large fluctuations in the prices of most of the commodities traded across different commodity markets in the world. It is quite interesting to state that gold is the one of the commodities showing the greatest resistance in terms of price stability. However the period from the beginning of 2008 witnessed large fluctuations in the price of gold across the world. It has made this commodity as one of the most preferred assets of investment. It further enhances the speculation over the price of gold in future. Though there has been an uptrend in the price of gold in general, it has undergone serious price fluctuations over the years. Hence, it is quite significant to examine the price discovery process during the periods of high volatility and how the price discovery is affected by volatility in spot and futures markets. Since the study covers the volatility impact of futures prices and spot prices on their returns, it has very high significance from the policy perspective. Besides, it supports all the different parties dealing with investment decisions pertaining to commodity markets. The price discovery analysis is of greater significance in the context of faster growth of Indian commodity market and increasing global integration among financial markets.
The transformation that happened to the commodity market brought in a number of changes like the arrival of new forms of trading and inclusion of new items of commodities which seem to have produced consequences as relative fluctuations in price, higher margins of profits to the participants and brokers involved in trading and so on. The price discovery process has been a matter of wide discussion among researchers and scholars. Though recent global meltdown witnessed large fluctuations in the prices of most of the commodities, gold was an exception with a strong resistance in terms of price stability. However, the period starting from 2008 witnessed lar ge fluctuations in the price of gold across the world . The same trend has been continuing even now . At present the price of gold has gone up to record breaking a height which has paved the way for huge speculation in its trading. Thus, it is very important to observe the nature of relationship between spot and futures markets. Also it is a key aspect to examine the price discovery process during price fluctuations in the market. Further, this scenario offers a significant area of research as to see the volatility effect of spot and futures market prices on the returns .
To analyse the price discovery process of gold in Indian commodity market
To examine the long run dynamic relationship between spot and futures markets
To observe the volatility effect of spot and futures market prices on returns
This empirical study is based on the secondary data collected from the official website of National Commodities Derivatives Exchange of India (NCDEX). The data analysis is carried out through appropriate statistical and econometric techniques. In order to make the time series data stationary, the Augmented Dickey Fuller test is used. The long run dynamic relationship between the futures and spot prices is examined through the Johansen co-integration technique. The analysis of price discovery is carried out with the help of Vector Error Correction Model (VECM) model. Further, the volatility impact of futures and spot prices on the returns, the Generalized Autoregressive Conditional Heteroscedasticity (GARCH) model is used.
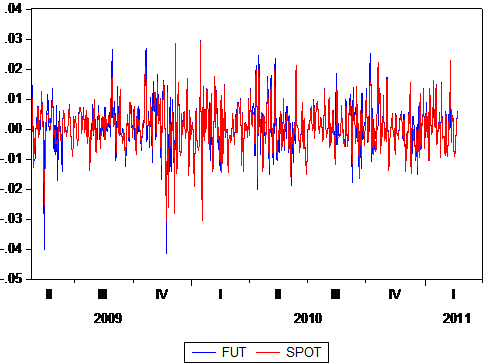
The spot and futures price of gold exhibit moderate volatility during the period of study. It shows that both of them follow the path of movement more or less in the same direction and magnitude. Thus it can be assumed that there is a good deal of interlink between these two markets. (Appendix: Figure 1)
Table No.1: Descriptive Statistics of Spot and Futures Markets
| FUTURE | SPOT | ||
| Mean | 0.000761 | Mean | 0.000768 |
| Median | 0.000744 | Median | 0.000509 |
| Maximum | 0.029472 | Maximum | 0.029167 |
| Minimum | -0.041514 | Minimum | -0.030697 |
| Std. Dev | 0.00858 | Std. Dev. | 0.008157 |
| Kurtosis | 5.505045 | Kurtosis | 4.513161 |
| Jarque-Bera | 131.1043 | Jarque-Bera | 46.13633 |
| Probability | 0 | Probability | 0 |
The descriptive statistics above shows that the sample means of spot and futures market returns are positive and the standard deviation ranges from 0.00858 (spot) to 0.00815 (futures). The values of skewness and excess kurtosis indicate that the distributions of spot and futures market returns are negatively skewed and leptokurtic relative to the normal distribution. The Jarque-Bera test statistic rejects normality at one per cent level of statistical significance in both cases.
The augmented Dickey-Fuller test (ADF) is the extension of the Dickey-Fuller (DF) test that removes all the structural effects (autocorrelation) in the time series data and then tests using the same procedure. ADF is a test for a unit root in a time series sample. It is an augmented version of the Dickey–Fuller test for a larger and more complicated set of time series models. The augmented Dickey–Fuller (ADF) statistic, used in the test, is a negative number. The more negative it is, the stronger the rejections of the hypothesis that there is a unit root at some level of confidence. Regressing non-stationary variables on each other leads to potentially misleading inferences about the estimated parameters and the degree of association. Therefore, before testing for co-integration, the order of integration of price series must be determined. To identify whether the series are I (1), the augmented Dickey-Fuller (ADF) test (Dickey and Fuller, 1979) is employed.
Augmented Dickey-Fuller Regression:
Δ Xt = ρ 0 + ρ Xt-1 + δ i Δ Xt-i + ε t (1)
Where Xt = the log price series, ρ 0 = a constant or drift , ρ = ( α - 1), Δ = the first difference operator, ε t = a pure white noise error term and Δ Xt-1 = (Xt-1 -Xt-2 ), Δ Xt-2 = Δ Xt-2 - Δ Xt-3 , etc ., i =1 to n is number of lagged difference terms which is determined empirically to remove any autocorrelation in error term ε t . The null hypothesis is to test that ρ =0. If ρ =0, then α =1, that is, there is a unit root, meaning the time series under consideration is non-stationary. But for stationarity, α must be less than one and hence ρ must be negative.
Augmented Dickey-Fuller regression:
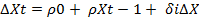 t
t
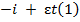
Where xt = the log price series, ρ 0 = a constant or drift , ρ = ( α - 1), Δ = the first difference operator, ε t = a pure white noise error term and Δ Xt-1 = (Xt-1 -Xt-2 ), Δ Xt-2 = Δ Xt-2 - Δ Xt-3 , and so on , i =1 to n is number of lagged difference terms which is determined empirically to remove any autocorrelation in error term ε t . The null hypothesis is to test that ρ =0. If ρ =0, then α =1, that is, there is a unit root, meaning the time series under consideration is non-stationary. But for stationarity, α must be less than one and hence ρ must be negative.
Table No.2: ADF Test Result
| Sl. No. | Variables | Intercept | Intercept & trend |
| I. Level | |||
| 1 | Future | -2.8661 (0.9297) | -3.417190 (0.4776) |
| 2 | Spot | -2.8661 (0.8199) | -3.4172 (0.1526) |
| II. First Difference | |||
| 1 | Future | -3.417190* 0 | -3.417737* 0 |
| 2 | Spot | -2.866401* (0.0000) | -3.417737* 0 |
|
Note: * – indicates significance at one per cent level.
The results reveal that both the data series are not stationary at the level but stationary after the first difference. It reveals that the time series has random walk effect which means there is information asymmetry in the market. It signifies that the market is a weakly efficient one. There are at least two advantages when using the first difference data series to explain the impulse response function. First, it focuses more on the increase or the decrease trend rather than the actual change. Second, it captures more information on the shocks of gold prices, because the first difference data shows the changes in the past two days while the level data shows the changes in one day in impulse response function. The long run dynamics between spot and futures markets of gold The Johansen co-integration test examines the co-integration of several time series. It examines the number of independent linear combinations (k) for an m time series variables set that yields a stationary process. It permits more than one cointegrating relationship. It has two forms, with trace or with maximum eigen value. It assumes the presence of common non-stationary (that is I(1)) processes underlying the input time series variables. |
|||
![\[ X_{1,t}=\alpha_1+\gamma_1Z_{1,t}+\gamma_2Z_{2,t}+\cdots+\gamma_pZ_{p,t}+\epsilon_{1,t} \]](2015_month/April/11/image006.png)
![\[ X_{2,t}=\alpha_2+\phi_1Z_{1,t}+\phi_2Z_{2,t}+\cdots+\phi_pZ_{p,t}+\epsilon_{2,t} \]](2015_month/April/11/image007.png)
![\[ X_{m,t}=\alpha_m+\psi_1Z_{1,t}+\psi_2Z_{2,t}+\cdots+\psi_pZ_{p,t}+\epsilon_{m,t} \]](2015_month/April/11/image008.png)
The number of independent linear combinations (k) is related to the assumed number of common non-stationary underlying processes (p) as p=m-k . The three plausible outcomes are given below.
1. k=0,p=m. In this case, time series variables are not cointegrated.
2. 0 < k < m, 0 < p < m. In this case, the time series variables are co-integrated.
3. k=m,p=m. All time-series variables are stationary I(0) to start with. Co-integration is not relevant here.
Table No.3: Johansen Co-integration Test
| Hypothesized | Trace | 0.05 | ||
| No. of CE(s) | Eigen value | Statistic | Critical Value | Prob.** |
| None * | 0.253228 | 232.2015 | 15.49471 | 0.0001 |
| At most 1 * | 0.180382 | 94.08767 | 3.841466 | 0.1832 |
| Trace test indicates 2 cointegrating equations at the 0.05 level | ||||
| * denotes rejection of the hypothesis at the 0.05 level | ||||
| **MacKinnon-Haug-Michelis (1999) p-values | ||||
Maximum Eigen value and Trace test statistics indicate the presence of one co-integrating vector between the spot and futures market prices at five per cent level. This shows that spot and futures prices of gold market are co-integrated and there exists utmost one co-integrating relationship between them. In other words, spot and futures prices share common long-run information.
Analysis of Price Discovery Process
The price discovery process is analysed through a vector error correction model (VECM). It adds error correction features to a multi-factor model such as a Vector Autoregression (VAR) model. In a frictionless market, security prices on the same underlying asset price should be perfectly correlated and that no lead-lag relationship would exist. When the price of one commodity leads the price of another commodity, we say that price is discovered in the first commodity. It implies that the first commodity responds fast to new information. Moreover, the price should be co-integrated, meaning despite short term deviations from each other, market forces will restore them in the long-run because the random walk component in their efficient prices are driven by the same fundamentals.
Engle and Granger (1987) showed the VECM representation for two co-integrated series as given below:
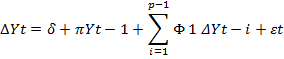
Where Δ is the differencing operator, such that
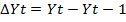
Table No.4: The Vector Error Correction Model
| Cointegrating Variables | Cointegrating equation | |
| S(-1) | 1.000000 | |
| F(-1) | -0.977552 | |
| (0.01316) | ||
| [-74.3037] | ||
| C | -428.2496 | |
| Error Correction: | D(S) | D(F) |
| Cointegrating Equation 1 | -0.124142 | -0.024935 |
| (0.03551) | (0.04322) | |
| [-3.49626] | [-0.57696] | |
| D(S(-1)) | -0.600438 | 0.202733 |
| (0.05984) | (0.07284) | |
| [-10.0333] | [ 2.78327] | |
| D(S(-2)) | -0.224046 | 0.150587 |
| (0.05113) | (0.06223) | |
| [-4.38201] | [ 2.41982] | |
| D(F(-1)) | 0.773375 | -0.107667 |
| (0.05439) | (0.06620) | |
| [ 14.2192] | [-1.62640] | |
| D(F(-2)) | 0.239519 | -0.267761 |
| (0.06154) | (0.07490) | |
| [ 3.89217] | [-3.57486] | |
| C | 11.66847 | 9.845516 |
| (7.65916) | (9.32229) | |
| [ 1.52347] | [ 1.05613] |
In the vector error correction estimates given above, the probability value is highly significant at 1 percent level. Also the co-integrating equation value is less than one for futures market. It signifies that spot market is dominant in the price discovery process. It is a clear indication that spot market of gold is information efficient in India. This could be attributed to the efficient transmission of information among traders in spot market as they tend to trade more frequently. The coefficients (DS and DF) of the error correction terms provide some insight into the adjustment process of spot and futures prices towards equilibrium in all types of contracts which means that the error correction terms represent a mean-reverting price process.
The volatility impact refers to the impact of spot and futures price fluctuations on spot and futures market returns. Financial time series often exhibit the phenomenon of volatility clustering, that is periods in which their prices show wide swings for an extended time period followed by periods in which there is relative calm. One of the important characteristics of financial time series is that in their level form they are random walks, that is they are non-stationary and in the first difference form they are generally stationary. But these first differences often exhibit wide swings, or volatility, suggesting that the variance of financial time series varies over time. In order to model these ‘varying variance’ the Genaralised Autoregressive Conditional Heteroscedasticity (GARCH) model is used. The GARCH equation can be written as follows:
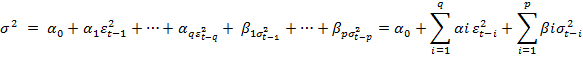
When dealing with time series data, heteroscedasticity implies to test for ARCH errors and GARCH errors.
Table No.5: The GARCH (1,1) Result
| Variable | Mean Equation | Variance Equation |
| C AR(1) | µ α β | |
| 10.087780.997822 | 0.000 0.045848 0.908893 | |
| 10.24164 0.998267 | 0.000 0.053470.914588 |
The table clearly shows the GARCH effect in both spot and futures market. The coefficient value is significant at 5% level. Since the probability value is zero, the null hypothesis is rejected which signifies the market is highly volatile. The value of variance of residual and the variance of GARCH equation clearly indicate that the volatility in independent variable (spot market) influences the dependent variable (futures market). It implies that both futures as well as spot do have significant impact in the price volatility of gold in India.
A major reason for the dominance of spot market in India can be the unprecedented volatility in the price of gold in recent years. This can be well connected with important investment premises. Investors and speculators are normally guided by expectations about future returns. The futures price will be determined by current price level along with future expectations. Investors may use the spot market to discover the prices applicable to futures contracts, which may be transmitted to the futures market. Greater efficiency of price discovery of spot market may help investors with more efficient strategies for hedging and speculating over the current price fluctuations. The insights from this would help the brokers and middlemen in reframing their future moves. It also guides in providing various customer services such as investment advice, consultancy and so on. For marketers, it provides a reliable forecast of spot prices in the future to effectively manage their risks in the production or marketing. They can evolve their long run strategies in the context of changing cost conditions and marketing strategies. Also it helps in evolving various strategies of hedging and arbitraging. The insights of the study can provide a strong support to international exporters and importers in evolving and modifying the strategies related to international operations.
From the policy front, the unprecedented uptrend in the price of gold and high volatility in recent years provides room for some important social implications. In India, jewellery demand plays a key role in the social life of people which in turn affects the consumption and saving of weaker sections of the society. It reminds the need of government intervention in safeguarding the interests of weaker sections. Further, a better understanding of the interconnectedness of the markets is useful for policy makers. Since the co-integration results uphold the long run dynamic relationship between futures and spot markets, any policy measure that affects the spot or futures market in particular will have a long run impact on the other. It implies that any policy change, directly or indirectly affects the financial market in general, will have its impact on both the markets. From the government policy point, it clearly signals for a better alternative to market intervention such as imposing price stabilization policies. It also indicates the need of proper control over insiders and noise traders from manipulating the commodity prices.
The study offers room for further research by extending the period under consideration so that clubbing the periods of normal and abnormal price increase will be possible which will help in reading the long run spot-futures relationship in a better way. It is also possible to look into other macroeconomic variables, such as exchange rate, changes in price level, changes in government policies and external sector influences on the volatility of gold prices. Since the jewellery demand is very huge, it is very apt to study the social implications or consequences of this abnormal price rise and volatility. Further, it is also interesting to look at some other commodities for which there are similar trends and see whether the results are in line with the results of gold.
Day Kushankur, & Maitra Debasish. (2012). Price discovery in Indian commodity futures market: An empirical exercise. International Journal of Trade and Global Markets, 5 (1) , 68-87.
Golaka.C.Nath, & Tulsi Lingareddy. (2012). Impact of futures trading on commodity prices. Economic and Political Weekly , 43 (3),18-23.
Srinivasan, P. (2012). Price discovery and volatility spillovers in Indian spot-futures commodity market. The IUP Journal of Behavioral Finance , 9 (1), 21-38.
Sarkar, A. K., &ShaileshRastogi. (2011). Impact of gold and silver futures on the spot rate volatility: An Indian perspective. Nice Journal of Business , 6 , 23-28.
Pantisa Pavabutr., & Piyamas Chaihetphon. (2010). Price discovery in Indian gold futures market. Journal of Economics and Finance , 5, 455-467.
VishwanathanIyer., & Archana Pillai. (2010). Price discovery and convergence in the Indian commodities market. Indian Growth and Development Review , 3 (1), 53-61.
Biswat Pratap Chandra. (2009). Price discovery in futures and spot commodity markets in India. Al-Barkaat Journal of Finance & Management , 1 (1), 21-44.
Salvadi Easwaran, R. & Ramasundaram, P. (2008). Whether commodity futures market in agriculture is efficient in price discovery? An econometric analysis. Agricultural Economics Research Review , 21 , 337-344.
Sahi, G. S. (2006). Influence of commodity derivatives on volatility of underlying; Working Paper, Indian Institute of Management (Lucknow), India.
Yang, J., Balyeat, B., & Leatham, D. J. (2005). Futures trading activity and commodity cash price volatility . Journal of Business Finance and Accounting , 32 , 297-323.
Zhong, Maosen, Ali F. Darrat., & Rafael Otero. (2004). Price discovery and volatility spillovers in index futures markets: Some evidence from Mexico. Journal of Banking and Finance , 28 , 3037- 3054.
M. T. Raju., & Kiran Karande. (2003). Price discovery and volatility on NSE futures market. NSE Working Paper Series, No.7.
Damodar. N. Gujarati, Dawn. C. Porter & Sangeeta Gunasekar. (2012). Basic Econometrics . Fifth Edition, New York: Tata McGraw-Hill.
Christopher, D. (2007). Introduction to Econometrics . Third Edition, New York: Oxford University Press.
Appendix:
Figure 1: The spot and future price movement: