|
Seyed Hasan Hataminasab Department of Business Management Yazd Branch, Islamic Azad University Yazd, Iran Email: Hataminasab@iauyazd.ac.ir |
Seyed Mohsen Mirjalili Department of Industrial Management Yazd Branch, Islamic Azad University Yazd, Iran Email: mohsenmirjalili23@yahoo.com |
Mahdieh Yavari Department of Industrial Management Yazd Branch, Islamic Azad University Yazd, Iran Email: m_yavari88@yahoo.com |
Mohamadreza Pakdel Department of Business Management Yazd Branch, Islamic Azad University Yazd, Iran Email: pakdel_manager@yahoo.com |
The staffing schedule according to the objectives of the system and minimizing the cost of production is among the most important factors in productivity. Manpower planning as the means of ensuring the human resources needed to achieve the organization's goals and its mathematical modeling is important for planners. Given that to solve staffing timing issue is very time consuming, in this paper, genetic algorithm is used to solve the proposed model. Therefore, many mathematical models have been used to formulate the scheduling in organizations and through a variety of methods have been tried to solve them. Considering the absence right for the personnel is one of the advantages of the proposed model. Since the cost is regarded as damage, the problem has changed to the cover mode. First, parameters and all restrictions are included with respect to information of the problem and modeling is implemented; then, the problem is solved with genetic algorithm. Finally, results of computations obtained based on different evaluations about the personnel’s number suggest that in the given problem, 90 personnel can satisfy restrictions and reduce penalties at the best.
Key words: staff scheduling, genetic algorithm, work pattern, mathematical modeling.
Scheduling is a tool for optimal use of available resources. Resources and jobs may have various types in scheduling and along with the development of industrial world the resources become more critical (1). The timing of the resources leads to the increase of the efficiency and utilization of capacity, reduction of the time required to complete tasks and ultimately the increase profitability of an organization. Scheduling is the allocation process of resources limited to activities over time and optimization of one or more objective function. Resources include manpower, machines, materials, auxiliary equipment etc. Appropriate scheduling of resources such as machines and human resources must be considered as a necessity in today's competitive environment (2).
For modeling optimization problems the problem should be described by mathematical variables and relations so that the optimization problem to be simulated. A general and initial model of the scheduling can be of maximizing or minimizing types and can be defined as follows (3):
Based on the system requirements this model can be divided into different classes. Overall classification of the works done in the field of manpower planning in is defined by three particular species: (4)
1. Nurses' scheduling that conducted researches are according to the planning of nursing care and services provided by them in shifts and week days.
2. The crew scheduling on the basis of services provided by the working groups in subway stations, train, air and urban transportation services
3. Staff scheduling on the type of an individual's work shift
Anthony Wren in one of his papers studied in detail the topic of planning, scheduling and shift of work and the relationship between them (5). According to him, scheduling is to arrange the elements in a pattern of time or location in order to reach or approach the objectives so that limits associated with these elements are met completely or nearly (7,6).
Through the expansion and development of the planning model, Aklin evaluated three shifts with 30 nurses and then compared the results with the results of the Forbidden Search (by Dazland). Results were same in terms of the solution, but very different in terms of the flexibility (8).
There are few articles about the timing of railway crew by the use of genetic algorithm to solve problems. For example, articles written by Van et al or Kalyng Wood which are generally used for short distances (9).
A number of useful articles to review solving techniques of projects scheduling problems in case of limited resources have provided by Herolen et al (10).
Bukter has examined 21 innovative scheduling methods to solve the projects scheduling problem with limited resources (11). In addition, Bukter using critical path method and its computations has proposed a more precise innovative algorithm (12). In recent years, Nuter et al have investigated algorithms based on a factor to solve the mentioned problem and Lova et al have presented methods based on priority rules (13).
In 1997, Jen and Cheng showed that in genetic algorithm, to take the size of the initial population larger, the number of generations and crossing rate may result in expansion of the search space and consequently faster convergence of the algorithm (14). In 1999, Barndimart solved the problem of flexible process program with multi-objective function via a precise optimization algorithm. In the same year, Gedjati presented an approach compound of meta-heuristic methods on the basis of genetic algorithm to solve the problem FJS (15).
Burus and Mario in a paper titled as “Reconstruction of nurses’ scheduling: computational insight for the problem size parameters” tried to obtain insights and perceive outcomes and outputs of the nurses’ scheduling various strategies. Moreover, they considered limitation of the time and number of the nurses for adaption with the real conditions.
Iyonis et al in a paper titled as “The two-phase adaptive approach of neighborhood variables to schedule nurses” attempted to solve nurses’ scheduling problem using the search algorithm in two-phase variable neighborhood. In their research, at first in order to show efficiency it is recommended that the algorithm to be used for all nurses. Furthermore, according to evaluations, better results have achieved in the samples and the available approach distinguishes itself from other methods (17).
Komarodinet al in an article titled as “Quality problem of manpower tasks list- a methodology to solve tasks list quality by modification of the personnel structure” attempted to at first introduce quality problem of manpower tasks list and then to implement a three-stage methodology which is capable to assess personnel structure quality in order to achieve a high-quality personnel tasks list relying on current tasks algorithm. Based on the results, certain changes have been suggested in personnel levels. Results also emphasize that the three-stage algorithm refers to better personnel structures about adaption with the tasks list (18).
In another research titled as “An evolutionary approach to nursing task list” Burus and Mario suggest a meta-heuristic evolutionary method to solve the problem of nursing task program and indicate that how the proposed method operates continually in different situations (19).
Mehran and Ashuk in their study titled as “"Integer linear programming - exploration-based for heterogeneous scheduling, part-time workers” tried to at first determine the personnel work shifts appropriately and then assign the personnel according to a suitable scheduling program. To do this, they use integer linear programming. Moreover, they compared the results obtained randomly with the reference article and proved the strength of the model (20).
Tesayand Lee in a paper titled as “Two-phase modeling using genetic algorithm to solve nursing scheduling” with the consideration of requirements, government regulations and nurses’ shift preferences, at first arranged nurses’ work and their vacation and via the genetic algorithm solved and optimized scheduling as well as investigated any shift nurses’ violation of government regulations, applied hospital management requirements and a fair schedule. At the second stage, a list of nursing program was arranged and genetic algorithm to solve the optimized program was proved. Results have shown that this algorithm is a suitable tool to solve nursing schedule program. In addition, it can easily modify different issues the hospital encounters (21).
The studied model considers the absence right to reduce costs. The problem definition is as the following: weekly scheduling is done for n personnel at s day shift so that the staff are divided into work teams, any staff work time is represented by c*t day at a cycle of C and scheduling is done based on the three factors of worker absence, weekly need and cost reduction with regard to the firm weekly need to the staff.
· Assumptions of the mathematical programming model for staff scheduling is as follows:
ü The number of personnel is determined.
ü The number of work teams is determined.
ü The staff degree is clear.
ü Amount of the demand for any day shift is clear.
ü The number of day working shifts is determined.
ü Duration of each cycle is specified.
ü The number of the head operator is also specified for each system.
ü The cost of not covered demand is clear.
ü The cost of the additional operator is identified.
ü The cost of each team is determined.
ü Non-coverage cost of each individual's day shift is determined.
• Model objectives:
The main objective is to minimize all costs as follows:
1. Non-coverage cost of each individual's day shift
2. The cost of each team
3. The cost of not covered demand
4. The cost of the additional head operator
The aim of the model is to develop a work pattern for each individual model with minimal additional costs to the system.
• integer programming formulation:
}I} = Representative of the operator
{K}- The representative of the personnel degree, k = 1, ....,Deg
}J} = The representative of day work shift, j = 1, ...., C * t
}T} = The representative of shift t = 1, ..., s
{H}= The representative of the team, H = 1, ...., TIM
}C} = The representative of the work cycle
• Decision variables:
I XIJ -1 - person I is assigned to the day shift J with staff degree of k or 0 otherwise.
O1-1- The person I is the senior staff. Or 0 otherwise
fIh- 1- The person I is associated with the team h. Or 0 otherwise
• Parameters:
{N} = the number of operators
{D} = the number of degrees
{S} = number of shifts
{TIM} = number of teams
{DJk} = the day shift J demand for personnel with degree k
{SHIFTI} = number of current working day shifts for personnel I
{WDEMAND} = weight of the demand
{WHEAD} = weight of the operator
{WTEAM} = weight of the team
{Wdeg} = coefficient of degree
The proposed model:
S.t
The proposed algorithm
In many science and engineering problems commonly we face an objective function that we want to optimize it. Engineering issues are analyzed with different methods. Genetic algorithm can be classified as a numerical method, direct and random search. Genetic algorithm is a searching technique for solving problems using genetic model. This algorithm is one of the population-based algorithms which its basic idea is driven from the evolution theory. Genetic algorithm is of the most powerful and widely used algorithms in search and optimization problems. One reason for the popularity of the genetic algorithm is that it does not require a high level of advanced mathematical models. These algorithms follow the law of development. The evolution is performed by chromosomes intercourse and the mutation is done on them and chromosomes with more fitness have more chance to be transferred to the future generations (22).
Total flow of the genetic algorithm
To be based on population means that more than one solution is considered in any iteration. The set of solutions examined in any iteration is called a population of solutions. Rules and recipes of genetic algorithm are in such a way that the population of any iteration leads to the definition or creation of the next iteration of the population. It should be noted that initial solutions of the population could be selected at random from the area justified or created by innovative methods. Children of birth may lead to solutions better or worse than their parents. Acceptance of worse solutions as the new generation's solutions depends on an approach that is used to implement the genetic algorithm. In some approaches only those solutions are accepted that are better than their parents and in some cases worse responses are transmitted to future population. This process of generating new populations of the previous one continues until the algorithm stops (23).
Steps of the algorithm are as follows:
1 - The Beginning: Create a population of n chromosomes randomly.
2. Valuation: Evaluate fitness of f (x) of each chromosome x in the population.
3. New population: Form a new population. Repeat these steps until the new population is complete:
Selection: Select two chromosomes from the population according to their fitness.
Composition: Regarding the possibility of composition, combine parents to form new children.
Mutation: Regarding the possibility of mutation, mutate children at any position of chromosome.
Approve: Include new children in the new population.
Replacement: Apply the new population for process of the algorithm.
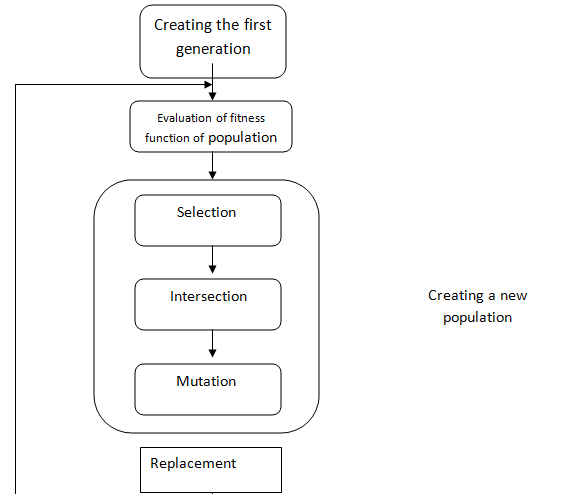
Figure1. Total flow of the genetic algorithm
The algorithm is proposed to solve the presented genetic model coded via MATLAB software and will be used to extract the model solutions.
1. Solutions structure with chromosome and creating the initial population:
In this study, for coding efficiency and increasing understanding of the problem a matrix structure similar to figure 1 is used to display the solution. Each column represents zero and a work shift and each row represents a certain staff schedule. Due to the nature of decision variables xij, answer of a matrix is zero and one. The amount of 1 to xij represents assignment of shifts j to individual i and the size of the matrix is in accordance with the number of individuals multiplied by the number of current shifts. In the model problem 21=7*3 and N=X; hence, the matrix is X * 21.

Figure2. Structure of the answer
Columns 1 to 3 represent 3 shifts of Saturday, 4 to 6 represent 3 shifts of Sunday and so on until columns 19 to 21 that represent 3 shifts of Friday. Since each staff has to work a shift per day, to satisfy the relation 5 the sum of each row should be 7 and values of zero and for 3 columns should be created once. To satisfy the relation 6 the columns sum should be 30 demands per day. Any chromosome which satisfies the relations 5 and 6 will be considered as a possible chromosome and then to satisfy relations 7, 8 and 9 we assign numbers 1 to 5 to sections of the matrix zero and 1 with the amount 1 so that 6 individuals to be allocated to each team. Next, numbers 1 and 2 is assigned as degree to the matrix satisfied the relation 7 so that at to each column only one of 1 to be belonged as the head operator and the relations 8 to 9 to be satisfied. Considering this method, to solve the problem limitations are satisfied automatically and the solution providing the lowest cost is considered as the problem solution.
2. Genetic algorithm operators
2-1. Intersection operator
To generate new chromosomes is the basis of the intersection operator. For this, vertical intersection operator has been used. A random number was generated in the interval satisfaction degree of the relation 5 will be effective and then the problematic chromosomes should be re-balanced.
2-2. Mutation operator
Mutation operator is mostly to transform. Therefore, two numbers are selected in intervals and for values i and j. If the selected xij is zero, it will be transformed to 1 and if xij is 1, it will be transformed to zero. Then, only the satisfaction degree of relations 5 and 6 may become problematic that should be modified.
3. How to select the parent population
To select the parent population, normalization method has been applied to the present generation living. Normalization is done as the following:
Where represents standard deviation of generation g and rpresents the chromosome i life in generation g.
The parent population involves those chromosomes that the value of is non-zero.
4. Stop criterion
To stop the algorithm, the below criteria is used:
1-Maximum of the generations
2- Minimum value of the generation allowed variance
Whenever one of the criteria is satisfied, the algorithm will stop.
4-1. Parameters included in genetic algorithm:
Table1. Parameters included in genetic algorithm:
| Maximum generation number | The number of each generation population | Minimum variance | Maximum allowed need (second) |
| 1000 | 200 | 5 | 3600 |
4-2. Computational results
To solve the model, a real problem with the below specifications was used that is presented by table.
According to the problem internal parameters, we solved the intended problem with 45, 60, 75, 90 and 100 personnel. Computational results are as the following table:
Table2. Internal parameters of the problem
| Internal parameters of the problem | |
| The personnel number | X |
| Shift number | 3 |
| Time interval | 7 |
| Teams number | 5 |
| Degrees number | 2 |
| Team leaders number | 0.033 |
| Shifts demand | 30 |
| Shift weight | 10 |
| Head operator weight | 3 |
| Team weight | 5 |
| Degree coefficient | 3 |
In the present paper, an integerprogramming approach to solve a generalized manpower scheduling program has been presented as a new mathematical model with multi shifts mode and with the assumption of individuals’ personnel degree and coverage mode. In other words, in the case of an individual’s absence due to the inclusion of damage costs to the system, the model changes to the coverage mode. The proposed model was created regarding the problem parameters and then the genetic algorithm was applied in order to solve the model in a larger scale. All internal parameters of the problem were assumed definite. According to the problem and personnel values, we realized that involvement of 90 personnel and consideration of one shift for any personnel per day may cause the lowest cost, satisfy the model limitations better and decrease loses. Thus, it is suggested that in order to schedule the staff the firms should employ a meta- heuristicalgorithm like the genetic algorithm for a better decision; as well as, since human resource is considered as the organization’s capital, planners and designers of the human resource could schedule the personnel program through the identification and inclusion of different factors of scheduling and thus satisfy the staff and improve their consent and productivity of the organization.
Table3. Computational results
| problem | Personnel number | Objective function (cost) | Time (second) |
| 1 | 45 | 1713 | 1350 |
| 2 | 60 | 1472 | 533 |
| 3 | 75 | 1252 | 384 |
| 4 | 90 | 1019 | 138 |
| 5 | 100 | 1863 | 121 |
1. Adams, J., Balas, E., &Zawack, D. (1988). The shifting bottleneck procedure for jobshop scheduling. Management Science, 34(3), 391-401.
2. Tavakoli-Moghadam, R., Fatemi – Ghomi, S.M.T., Afsari, F. and Safari N. “A mathematical model for Manpower scheduling solved by tabu search”. Amirkabir J. of Science and Technology, Vol.16 , No. 61B, 2005. p.p. 13-22.
3. Asgharpour MJ. (1998). The book "linear programming" Tehran University Press.
4. Tavakkoli-Moghaddam, R. and Islami, Sh., (2006). Paper "presentation of a new mathematical model for staff scheduling and solving it using a genetic algorithm, ُsharifacademic- research journal, No. 36, pp. 21-31.
5. Wern, A., “Scheduling, time tabling and rostering-a special Relat", School of Computer studies, University of Leeds (1995).
6. Warner, D. and Prawda, J., “A mathematical programming model for scheduling nursing personnel in a hospital", Management Science, 19, pp. 411-422 (1972).
7. Miller, H., Pierskalla, W. and Rath, G., “Nurse scheduling using mathematical programming", Operations Research, 24, pp. 875-870 (1976).
8. Aickelin, U. and Dowlands, K.A., “Exploiting problem structure in a genetic algorithm approach to nurse rostering problem", Journal of Scheduling, 3, pp. 139-153 (2000).
9. Kwan, R.S.K., Wren, A. and Kwan, A.S.K., “Hybrid genetic algorithms for scheduling Bus and train driver", School of Computer Studies, University of Leeds (2000).
10. Herroelen, W., Demeulemeester, E., De Reyck, B., “Resource-Constrained Project Scheduling: a Survey of Recent Developments”, Computers & Operations Research, Vol. 25, 1998, pp. 279–302.
11. Boctor, F.F., “Heuristics for Scheduling Projects with Resource Restrictions and Several Resource–Duration Modes”, International Journal of Production Research, Vol. 31, 1993, pp. 2547–2558.
12. Boctor, F.F, “Resource-Constrained Project Scheduling by Simulated Annealing”, International Journal of Production Research, Vol. 34, 1996, pp. 2335–2351.
13. NotezKnotts, G., Dror, M., Hartman, B., “Agent-Based Project Scheduling”, IIE Transactions, Vol. 32, 2000. p.p 387-401.
14. Gen, M., Cheng, R., “Genetic Algorithms and Engineering Design”, John Wiley & Sons, (1997)
15. Brandimarte, P., “Theory and Methodology, Exploiting Process Plan Flexibility in Production Scheduling: A Multi-Objective Approach”, European Journal of Operational Research, 114, 1999, pp. 59-71.
16. BroosMaenhout, Mario Vanhoucke.” Reconstructing nurse schedules: Computational insights in the problem size parameters” Elsevier Journal, Omega 41 (2013) 903–918.
17. Ioannis X. Tassopoulos, Ioannis P. Solos, Grigorios N. Beligiannis.” Α two phase adaptive variable neighborhood approach for nurse rostering” Elsevier Journal, Computers &OperationsResearch60, (2015)150–169 .
18. Komarudin , Marie-Anne Guerry , Tim De Feyter , Greet VandenBerghe.” The roster quality staffing problem – A methodology for improving the roster quality by modifying the personnel structure” European Journal of Operational Research, 230 (2013) 551–562.
19. BroosMaenhout , Mario Vanhoucke.” An evolutionary approach for the nurse rerostering problem” Computers & Operations Research 38 (2011) 1400–1411.
20. MehranHojati, Ashok S. Patil.” An integer linear programming-based heuristic for scheduling heterogeneous, part-time service employees” European Journal of Operational Research 209 (2011) 37–50.
21. Sherman H.A. Li,Chang-Chun Tsai. ” A two-stage modeling with genetic algorithms for the nurse scheduling problem: Expert Systems with Applications”, 36, (2009), 9506–9512.
22. Monajjemi, AM., MasoodianNematbakhsh, N (2009). "Automatic timing table design for university courses using genetic algorithms", Faculty of Engineering, University of Isfahan, Educational Technology Journal, Volume 4, Issue 2, pp. 113-127.
23. Nasrsdrabady, AR.,Taghavi, N., (2004). The book "Introduction tometa-heuristic algorithm" ,Pendar-e Pars Publications.